Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 145, pp. 1-24.
Existence of multiple solutions to elliptic equations satisfying a
global eigenvalue-crossing condition
Duong Minh Duc, Loc Hoang Nguyen, Luc Nguyen
Abstract:
We study the multiplicity of solutions to the elliptic equation
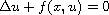 ,
under the assumption that
f(x,u)/u crosses globally but not pointwise
any eigenvalue for every x in a part of the domain,
when u varies from
,
under the assumption that
f(x,u)/u crosses globally but not pointwise
any eigenvalue for every x in a part of the domain,
when u varies from
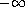 to
to
 .
Also we relax the conditions on uniform convergence of f(x,s)/s,
which are essential in many results on multiplicity for asymptotically
linear problems.
.
Also we relax the conditions on uniform convergence of f(x,s)/s,
which are essential in many results on multiplicity for asymptotically
linear problems.
Submitted April 10, 2013. Published June 25, 2013.
Math Subject Classifications: 47H11, 55M25, 35J20.
Key Words: Index of critical points; mountain pass type;
nonlinear elliptic equations; multiplicity of solutions.
Show me the PDF file (352 KB),
TEX file for this article.
 |
Duong Minh Duc
University of Sciences - Hochiminh City, Vietnam
email: dmduc@hcmuns.edu.vn
|
|---|
 |
Loc Hoang Nguyen
Department of Mathematics, Ecole Normale Suprieure
Paris, France
email: lnguyen@dma.ens.fr
|
|---|
| |
lu Nguyen
Department of Mathematics, Princeton University
Princeton, New Jersey 08544, USA
email: llnguyen@princeton.edu
|
|---|
Return to the EJDE web page
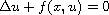 ,
under the assumption that
f(x,u)/u crosses globally but not pointwise
any eigenvalue for every x in a part of the domain,
when u varies from
,
under the assumption that
f(x,u)/u crosses globally but not pointwise
any eigenvalue for every x in a part of the domain,
when u varies from
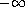 to
to
 .
Also we relax the conditions on uniform convergence of f(x,s)/s,
which are essential in many results on multiplicity for asymptotically
linear problems.
.
Also we relax the conditions on uniform convergence of f(x,s)/s,
which are essential in many results on multiplicity for asymptotically
linear problems.

