Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 177, pp. 1-13.
Energy quantization for approximate H-surfaces and applications
Shenzhou Zheng
Abstract:
We consider weakly convergent sequences of approximate H-surface maps
defined in the plane with their tension fields bounded in
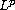 for
p> 4/3, and establish an energy quantization that accounts for
the loss of their energies by the sum of energies over finitely many
nontrivial bubbles maps on
for
p> 4/3, and establish an energy quantization that accounts for
the loss of their energies by the sum of energies over finitely many
nontrivial bubbles maps on
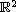 .
As a direct consequence,
we establish the energy identity at finite singular time to their
H-surface flows.
.
As a direct consequence,
we establish the energy identity at finite singular time to their
H-surface flows.
Submitted February 2, 2013. Published July 30, 2013.
Math Subject Classifications: 35J50, 35K40, 58D15.
Key Words: Approximate H-surface maps; energy quantization;
H-surface flows; concentration of energy; bubbling phenomena.
Show me the PDF file (272 KB),
TEX file for this article.
Shenzhou Zheng
Department of Mathematics,
Beijing Jiaotong University
Beijing 100044, China
email: shzhzheng@bjtu.edu.cn, Phone: +86-10-51688449
|
Return to the EJDE web page
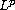 for
p> 4/3, and establish an energy quantization that accounts for
the loss of their energies by the sum of energies over finitely many
nontrivial bubbles maps on
for
p> 4/3, and establish an energy quantization that accounts for
the loss of their energies by the sum of energies over finitely many
nontrivial bubbles maps on
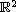 .
As a direct consequence,
we establish the energy identity at finite singular time to their
H-surface flows.
.
As a direct consequence,
we establish the energy identity at finite singular time to their
H-surface flows.