Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 180, pp. 1-8.
Existence of positive solutions for Kirchhoff type equations
Ghasem A. Afrouzi, Nguyen Thanh Chung,Saleh Shakeri
Abstract:
In this article, we are interested in the existence of positive
solutions for the Kirchhoff type problems
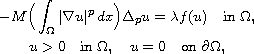
where
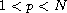 ,
,
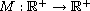 is a continuous and increasing
function,
is a continuous and increasing
function,
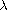 is a parameter,
is a parameter,
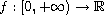 is a
is a
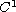 nondecreasing function satisfying
nondecreasing function satisfying
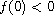 (semipositone).
Our proof is based on the sub- and super-solutions techniques.
(semipositone).
Our proof is based on the sub- and super-solutions techniques.
Submitted April 23, 2013. Published August 07, 2013.
Math Subject Classifications: 35D05, 35J60.
Key Words: Kirchhoff type problems; semipositone; positive solution;
sub-supersolution method.
Show me the PDF file (218 KB),
TEX file for this article.
 |
Ghasem Alizadeh Afrouzi
Department of Mathematics
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Nguyen Thanh Chung
Dept. Science Management and International Cooperation
Quang Binh University, 312 Ly Thuong Kiet
Dong Hoi, Quang Binh, Vietnam
email: ntchung82@yahoo.com
|
|---|
 |
Saleh Shakeri
Department of Mathematics
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: s.shakeri@umz.ac.ir
|
|---|
Return to the EJDE web page
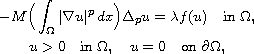
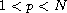 ,
,
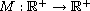 is a continuous and increasing
function,
is a continuous and increasing
function,
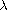 is a parameter,
is a parameter,
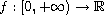 is a
is a
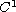 nondecreasing function satisfying
nondecreasing function satisfying
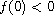 (semipositone).
Our proof is based on the sub- and super-solutions techniques.
(semipositone).
Our proof is based on the sub- and super-solutions techniques.


