For a Hurwitz stable matrix
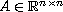 ,
we calculate the real structured radius of stability for
,
we calculate the real structured radius of stability for
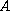 with a perturbation
with a perturbation
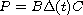 ,
where
,
where
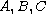 ,
,
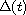 form a patterned
quadruple of matrices; i.e., they are polynomials of a common
matrix of simple structure
form a patterned
quadruple of matrices; i.e., they are polynomials of a common
matrix of simple structure
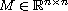 .
.
Henry Gonzalez
Abstract:
For a Hurwitz stable matrix
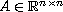 ,
we calculate the real structured radius of stability for
,
we calculate the real structured radius of stability for
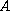 with a perturbation
with a perturbation
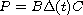 ,
where
,
where
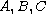 ,
,
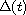 form a patterned
quadruple of matrices; i.e., they are polynomials of a common
matrix of simple structure
form a patterned
quadruple of matrices; i.e., they are polynomials of a common
matrix of simple structure
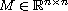 .
.
Submitted April 15, 2012. Published August 30, 2013.
Math Subject Classifications: 93D09, 34A60.
Key Words: Robust stability; stability radius.
Show me the PDF file (209 KB), TEX file for this article.
 |
Henry González Faculty of Light Industry and Environmental Protection Engineering Obuda University 1034 Budapest, Bécsiút 96/B, Hungary email: gonzalez.henry@rkk.uni-obuda.hu |
|---|
Return to the EJDE web page