Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 195, pp. 1-8.
Limit cycles for discontinuous generalized Lienard
polynomial differential equations
Jaume Llibre, Ana Cristina Mereu
Abstract:
We divide
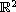 into sectors
into sectors
 ,
with
,
with
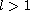 even,
and define a discontinuous differential system such that in each sector,
we have a smooth generalized Lienard polynomial differential equation
even,
and define a discontinuous differential system such that in each sector,
we have a smooth generalized Lienard polynomial differential equation
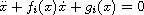 ,
,
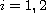 alternatively, where
alternatively, where
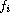 and
and
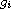 are polynomials of degree n-1 and m respectively.
Then we apply the averaging theory for first-order discontinuous differential
systems to show that for any
are polynomials of degree n-1 and m respectively.
Then we apply the averaging theory for first-order discontinuous differential
systems to show that for any
 and
and
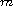 there are non-smooth Lienard polynomial
equations having at least max{n,m} limit cycles.
Note that this number is independent of the number of sectors.
there are non-smooth Lienard polynomial
equations having at least max{n,m} limit cycles.
Note that this number is independent of the number of sectors.
Submitted May 7, 2013. Published September 3, 2013.
Math Subject Classifications: 34C29, 34C25, 47H11.
Key Words: Limit cycles; non-smooth Lienard systems; averaging theory.
Show me the PDF file (221 KB),
TEX file for this article.
 |
Jaume Llibre
Departament de Matematiques
Universitat Autonoma de Barcelona
08193 Bellaterra, Barcelona, Catalonia, Spain
email: jllibre@mat.uab.cat
|
|---|
 |
Ana Cristina Mereu
Department of Physics, Chemistry and Mathematics
UFSCar 18052-780, Sorocaba, SP, Brazil
email: anamereu@ufscar.br
|
|---|
Return to the EJDE web page
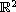 into sectors
into sectors
 ,
with
,
with
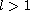 even,
and define a discontinuous differential system such that in each sector,
we have a smooth generalized Lienard polynomial differential equation
even,
and define a discontinuous differential system such that in each sector,
we have a smooth generalized Lienard polynomial differential equation
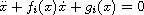 ,
,
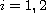 alternatively, where
alternatively, where
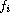 and
and
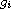 are polynomials of degree n-1 and m respectively.
Then we apply the averaging theory for first-order discontinuous differential
systems to show that for any
are polynomials of degree n-1 and m respectively.
Then we apply the averaging theory for first-order discontinuous differential
systems to show that for any
 and
and
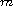 there are non-smooth Lienard polynomial
equations having at least max{n,m} limit cycles.
Note that this number is independent of the number of sectors.
there are non-smooth Lienard polynomial
equations having at least max{n,m} limit cycles.
Note that this number is independent of the number of sectors.

