Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 197, pp. 1-14.
Subharmonic solutions for first-order Hamiltonian systems
Mohsen Timoumi
Abstract:
In this article, we study the existence of periodic and subharmonic
solutions for a class of non-autonomous first-order Hamiltonian systems
such that the nonlinearity has a growth at infinity
faster than
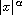 ,
,
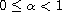 .
We also study the minimality of periods for such solutions.
Our results are illustrated by specific examples.
The proofs are based on the least action principle and a generalized
saddle point theorem.
.
We also study the minimality of periods for such solutions.
Our results are illustrated by specific examples.
The proofs are based on the least action principle and a generalized
saddle point theorem.
Submitted March 31, 2013. Published September 5, 2013.
Math Subject Classifications: 34C25.
Key Words: Hamiltonian systems; periodic solutions; subharmonic;
minimal periods; generalized saddle point theorem.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Mohsen Timoumi
Department of Mathematics
Faculty of Sciences, 5000 Monastir, Tunisia
email: m_timoumi@yahoo.com
|
|---|
Return to the EJDE web page
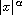 ,
,
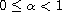 .
We also study the minimality of periods for such solutions.
Our results are illustrated by specific examples.
The proofs are based on the least action principle and a generalized
saddle point theorem.
.
We also study the minimality of periods for such solutions.
Our results are illustrated by specific examples.
The proofs are based on the least action principle and a generalized
saddle point theorem.
