Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 214, pp. 1-12.
Ground state solutions for semilinear problems with a Sobolev-Hardy term
Xiaoli Chen, Weiyang Chen
Abstract:
In this article, we study the existence of solutions to the problem

where
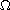 is a smooth bounded domain in
is a smooth bounded domain in
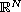
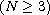 .
We show that there is a ground state solution provided that N=4 and
.
We show that there is a ground state solution provided that N=4 and
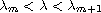 ,
or that
,
or that
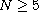 and
and
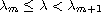 ,
where
,
where
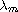 is the m'th eigenvalue of
is the m'th eigenvalue of
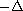 with Dirichlet boundary
conditions.
with Dirichlet boundary
conditions.
Submitted April 19, 2013. Published September 26, 2013.
Math Subject Classifications: 35J60, 35J65.
Key Words: Existence; ground state; critical Hardy-Sobolev exponent;
semilinear Dirichlet problem.
Show me the PDF file (250 KB),
TEX file for this article.
 |
Xiaoli Chen
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: littleli_chen@163.com
|
|---|
 |
Weiyang Chen
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: xiaowei19901207@126.com
|
|---|
Return to the EJDE web page

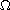 is a smooth bounded domain in
is a smooth bounded domain in
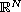
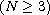 .
We show that there is a ground state solution provided that N=4 and
.
We show that there is a ground state solution provided that N=4 and
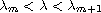 ,
or that
,
or that
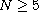 and
and
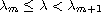 ,
where
,
where
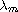 is the m'th eigenvalue of
is the m'th eigenvalue of
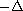 with Dirichlet boundary
conditions.
with Dirichlet boundary
conditions.

