Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 264, pp. 1-17.
Blowup and existence of global solutions to nonlinear
parabolic equations with degenerate diffusion
Zhengce Zhang, Yan Li
Abstract:
In this article, we consider the degenerate parabolic equation
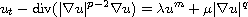
on a smoothly bounded domain
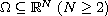 ,
with homogeneous Dirichlet boundary conditions. The values of
,
with homogeneous Dirichlet boundary conditions. The values of
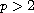 ,
,
 and
and
 will vary in different circumstances, and the
solutions will have different behaviors.
Our main goal is to present the sufficient conditions for
will vary in different circumstances, and the
solutions will have different behaviors.
Our main goal is to present the sufficient conditions for
 blowup,
for gradient blowup, and for the existence of global solutions.
A general comparison principle is also established.
blowup,
for gradient blowup, and for the existence of global solutions.
A general comparison principle is also established.
Submitted January 18, 2013. Published November 29, 2013.
Math Subject Classifications: 35A01, 35B44, 35K55, 35K92.
Key Words: Degenerate parabolic equation; L-infinity blowup; gradient blowup;
global solution; comparison principle.
Show me the PDF file (330 KB),
TEX file for this article.
 |
Zhengce Zhang
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an 710049, China
email: zhangzc@mail.xjtu.edu.cn
|
 |
Yan Li
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an 710049, China
email: liyan1989@stu.xjtu.edu.cn
|
Return to the EJDE web page
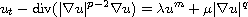
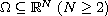 ,
with homogeneous Dirichlet boundary conditions. The values of
,
with homogeneous Dirichlet boundary conditions. The values of
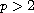 ,
,
 and
and
 will vary in different circumstances, and the
solutions will have different behaviors.
Our main goal is to present the sufficient conditions for
will vary in different circumstances, and the
solutions will have different behaviors.
Our main goal is to present the sufficient conditions for
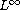 blowup,
for gradient blowup, and for the existence of global solutions.
A general comparison principle is also established.
blowup,
for gradient blowup, and for the existence of global solutions.
A general comparison principle is also established.

