Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 82, pp. 1-11.
Positive solutions and global bifurcation of strongly coupled elliptic systems
Jagmohan Tyagi
Abstract:
In this article, we study the existence of positive solutions for
the coupled elliptic system
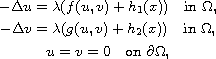
under certain conditions on
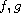 and allowing
and allowing
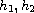 to be singular.
We also consider the system
to be singular.
We also consider the system
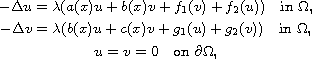
and prove a Rabinowitz global bifurcation type theorem to this system.
Submitted April 18, 2012. Published March 31, 2013.
Math Subject Classifications: 35J57, 35B32, 35B09.
Key Words: Elliptic system; bifurcation; positive solutions.
Show me the PDF file (249 KB),
TEX file for this article.
 |
Jagmohan Tyagi
Indian Institute of Technology Gandhinagar
Vishwakarma Government Engineering College Complex
Chandkheda, Visat-Gandhinagar Highway, Ahmedabad
Gujarat, India, 382424
email: jtyagi1@gmail.com, jtyagi@iitgn.ac.in
|
|---|
Return to the EJDE web page
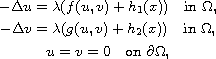
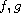 and allowing
and allowing
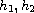 to be singular.
We also consider the system
to be singular.
We also consider the system