Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 03, pp. 1-10.
Bifurcation from intervals for Sturm-Liouville problems and its applications
Guowei Dai, Ruyun Ma
Abstract:
We study the unilateral global bifurcation for the nonlinear
Sturm-Liouville problem
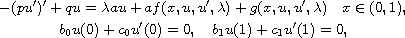
where
![$a\in C([0, 1], [0,+\infty))$](gifs/ab.gif) and
and
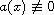 on any subinterval of
on any subinterval of
![$[0, 1]$](gifs/ad.gif) ,
,
![$f,g\in C([0,1]\times\mathbb{R}^3,\mathbb{R})$](gifs/ae.gif) and f is
not necessarily differentiable at the origin or infinity with respect to u.
Some applications are given to nonlinear second-order two-point boundary-value
problems. This article is a continuation of [8].
and f is
not necessarily differentiable at the origin or infinity with respect to u.
Some applications are given to nonlinear second-order two-point boundary-value
problems. This article is a continuation of [8].
Submitted September 8, 2013. Published January 3, 2014.
Math Subject Classifications: 34B24, 34C10, 34C23.
Key Words: Global bifurcation; nodal solutions; eigenvalues.
Show me the PDF file (246 KB),
TEX file for this article.
 |
Guowei Dai
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: daiguowei@nwnu.edu.cn
|
|---|
 |
Ruyun Ma
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: mary@nwnu.edu.cn
|
Return to the EJDE web page
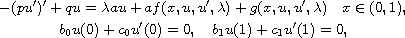
![$a\in C([0, 1], [0,+\infty))$](gifs/ab.gif) and
and
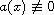 on any subinterval of
on any subinterval of
![$[0, 1]$](gifs/ad.gif) ,
,
![$f,g\in C([0,1]\times\mathbb{R}^3,\mathbb{R})$](gifs/ae.gif) and f is
not necessarily differentiable at the origin or infinity with respect to u.
Some applications are given to nonlinear second-order two-point boundary-value
problems. This article is a continuation of [8].
and f is
not necessarily differentiable at the origin or infinity with respect to u.
Some applications are given to nonlinear second-order two-point boundary-value
problems. This article is a continuation of [8].

