In this article we consider the normalized one-dimensional three-wave interaction model
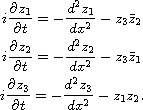
Solitary waves for this model are solutions of the form
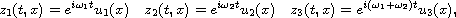
where
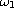 and
and
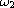 are positive frequencies, and
are positive frequencies, and
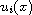 ,
,
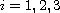 are real-valued functions that satisfy the ODE system
are real-valued functions that satisfy the ODE system

For the case
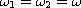 , we prove existence,
uniqueness and stability of solitary waves corresponding
to positive solutions
, we prove existence,
uniqueness and stability of solitary waves corresponding
to positive solutions
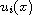 that tend to zero as x tends to infinity.
The full model has more parameters, and the case we consider
corresponds to the exact phase matching. However, as we will see,
even in the simpler case, a formal proof of stability depends on
a nontrivial spectral analysis of the linearized operator.
This is so because the spectral analysis depends on some calculations
on a full neighborhood of the parameter
that tend to zero as x tends to infinity.
The full model has more parameters, and the case we consider
corresponds to the exact phase matching. However, as we will see,
even in the simpler case, a formal proof of stability depends on
a nontrivial spectral analysis of the linearized operator.
This is so because the spectral analysis depends on some calculations
on a full neighborhood of the parameter
 and the solution
is not known explicitly.
and the solution
is not known explicitly.
