Joan C. Artes, Jaume Llibre, Dana Schlomiuk, Nicolae Vulpe
Abstract:
In this work we consider the problem of classifying all
configurations of singularities, both finite and infinite of
quadratic differential systems, with respect to the
geometric equivalence relation defined in [3].
This relation is deeper than the topological equivalence relation
which does not distinguish between a focus and a node or between a
strong and a weak focus or between foci of different orders.
Such distinctions are however important in the production of limit
cycles close to the foci in perturbations of the systems. The notion of
geometric equivalence relation of configurations of singularities
allows to incorporates all these important geometric
features which can be expressed in purely algebraic terms. This
equivalence relation is also deeper than the qualitative equivalence
relation introduced in [17]. The geometric classification of all
configurations of singularities, finite and infinite, of quadratic
systems was initiated in [4] where the classification was done for
systems with total multiplicity
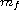 of finite singularities less
than or equal to one. In this article we continue the work initiated
in [4] and obtain the geometric classification of singularities, finite and
infinite, for the subclass of quadratic differential systems
possessing finite singularities of total multiplicity
of finite singularities less
than or equal to one. In this article we continue the work initiated
in [4] and obtain the geometric classification of singularities, finite and
infinite, for the subclass of quadratic differential systems
possessing finite singularities of total multiplicity
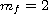 .
We obtain 197 geometrically distinct configurations of
singularities for this family. We also give here the global
bifurcation diagram of configurations of singularities, both
finite and infinite, with respect to the geometric equivalence relation,
for this class of systems. The bifurcation set of this diagram is algebraic.
The bifurcation diagram is done in the 12-dimensional space of parameters
and it is expressed in terms of polynomial invariants. The results can
therefore be applied for any family of quadratic systems in this class,
given in any normal form. Determining the geometric configurations of
singularities for any such family, becomes thus a simple task
using computer algebra calculations.
.
We obtain 197 geometrically distinct configurations of
singularities for this family. We also give here the global
bifurcation diagram of configurations of singularities, both
finite and infinite, with respect to the geometric equivalence relation,
for this class of systems. The bifurcation set of this diagram is algebraic.
The bifurcation diagram is done in the 12-dimensional space of parameters
and it is expressed in terms of polynomial invariants. The results can
therefore be applied for any family of quadratic systems in this class,
given in any normal form. Determining the geometric configurations of
singularities for any such family, becomes thus a simple task
using computer algebra calculations.
Submitted November 25, 2013. Published July 18, 2014.
Math Subject Classifications: 58K45, 34C05, 34A34.
Key Words: Quadratic vector fields; infinite and finite singularities;
affine invariant polynomials; Poincare compactification;
configuration of singularities; geometric equivalence relation.
Show me the PDF file (2462 KB), TEX file for this article.
 |
Joan C. Artés Departament de Matemátiques Universitat Autónoma de Barcelona 08193 Bellaterra, Barcelona, Spain email: artes@mat.uab.cat |
|---|---|
 |
Jaume Llibre Departament de Matemátiques Universitat Autónoma de Barcelona 08193 Bellaterra, Barcelona, Spain email: jllibre@mat.uab.cat |
 |
Dana Schlomiuk Département de Mathématiques et de Statistiques Université de Montréal, Canada email: dasch@dms.umontreal.ca |
 |
Nicolae Vulpe Institute of Mathematics and Computer Science Academy of Science of Moldova 5 Academiei str, Chisinau, MD-2028, Moldova email: nvulpe@gmail.com |
Return to the EJDE web page