Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 162, pp. 1-12.
Isochronous bifurcations in second-order delay differential equations
Andrea Bel, Walter Reartes
Abstract:
In this article we consider a special type of second-order delay
differential equations. More precisely, we take an equation of a conservative
mechanical system in one dimension with an added term that is a function of the
difference between the value of the position at time t minus the position at
the delayed time
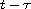 .
For this system, we show that, under certain
conditions of non-degeneration and of convergence of the periodic solutions
obtained by the Homotopy Analysis Method, bifurcation branches appearing in
a neighbourhood of Hopf bifurcation due to the delay are isochronous; i.e.,
all the emerging cycles have the same frequency.
.
For this system, we show that, under certain
conditions of non-degeneration and of convergence of the periodic solutions
obtained by the Homotopy Analysis Method, bifurcation branches appearing in
a neighbourhood of Hopf bifurcation due to the delay are isochronous; i.e.,
all the emerging cycles have the same frequency.
Submitted November 4, 2013. Published July 24, 2014.
Math Subject Classifications: 34K13, 34K18
Key Words: Delay differential equations; Hopf bifurcation; isochronous cycles.
Show me the PDF file (383 KB),
TEX file for this article.
 |
Andrea Bel
Universidad Nacional del Sur
Av. Alem 1253, 8000 Bahía Blanca
Buenos Aires, Argentina
email: andrea.bel@uns.edu.ar
|
|---|
 |
Walter Reartes
Universidad Nacional del Sur
Av. Alem 1253, 8000 Bahía Blanca
Buenos Aires, Argentina
email: walter.reartes@gmail.com
|
|---|
Return to the EJDE web page
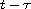 .
For this system, we show that, under certain
conditions of non-degeneration and of convergence of the periodic solutions
obtained by the Homotopy Analysis Method, bifurcation branches appearing in
a neighbourhood of Hopf bifurcation due to the delay are isochronous; i.e.,
all the emerging cycles have the same frequency.
.
For this system, we show that, under certain
conditions of non-degeneration and of convergence of the periodic solutions
obtained by the Homotopy Analysis Method, bifurcation branches appearing in
a neighbourhood of Hopf bifurcation due to the delay are isochronous; i.e.,
all the emerging cycles have the same frequency.

