Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 183, pp. 1-12.
Exact boundary behavior of solutions to
singular nonlinear Dirichlet problems
Bo Li, Zhijun Zhang
Abstract:
In this article we analyze the exact boundary behavior of solutions
to the singular nonlinear Dirichlet problem
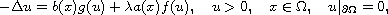
where
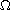 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
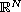 ,
,
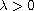 ,
,
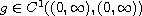 ,
,
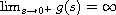 ,
,
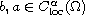 ,
are positive, but may vanish or be singular on the boundary,
and
,
are positive, but may vanish or be singular on the boundary,
and
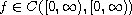 .
.
Submitted July 11, 2014. Published August 29, 2014.
Math Subject Classifications: 35J65, 35B05, 35J25, 60J50.
Key Words: Semilinear elliptic equation; singular Dirichlet problem;
positive solution; boundary behavior.
Show me the PDF file (261 KB),
TEX file for this article.
 |
Bo Li
School of Mathematics and Statistics,
Lanzhou University
Lanzhou 730000, Gansu, China
email: libo_yt@163.com
|
|---|
 |
Zhijun Zhang
School of Mathematics and Information Science
Yantai University, Yantai 264005, Shandong, China
email: chinazjzhang2002@163.com, zhangzj@ytu.edu.cn
|
|---|
Return to the EJDE web page
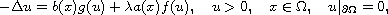
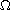 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
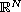 ,
,
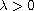 ,
,
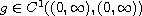 ,
,
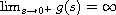 ,
,
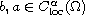 ,
are positive, but may vanish or be singular on the boundary,
and
,
are positive, but may vanish or be singular on the boundary,
and
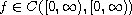 .
.

