Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 217, pp. 1-16.
Stability of traveling-wave solutions for a Schrodinger system
with power-type nonlinearities
Nghiem V. Nguyen, Rushun Tian, Zhi-Qiang Wang
Abstract:
In this article, we consider the Schrodinger system with
power-type nonlinearities,
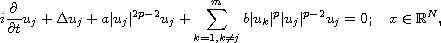
where
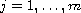 ,
,
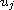 are complex-valued functions of
are complex-valued functions of
 ,
a,b are real numbers. It is shown that when
,
a,b are real numbers. It is shown that when
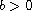 , and
, and
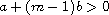 ,
for a certain range of p, traveling-wave solutions of this system exist,
and are orbitally stable.
,
for a certain range of p, traveling-wave solutions of this system exist,
and are orbitally stable.
Submitted November 22, 2013. Published October 16, 2014.
Math Subject Classifications: 35A15, 35B35, 35Q35, 35Q55.
Key Words: solitary wave solutions; stability; nonlinear Schrodinger system;
traveling-wave solutions
Show me the PDF file (294 KB),
TEX file for this article.
 |
Nghiem V. Nguyen
Department of Mathematics and Statistics
Utah State University, Logan, UT 84322, USA
email: nghiem.nguyen@usu.edu
|
|---|
 |
Rushun Tian
Academy of Mathematics and System Science
Chinese Academy of Sciences
Beijing 100190, China
email: rushun.tian@amss.ac.cn
|
|---|
| |
Zhi-Qiang Wang
Department of Mathematics and Statistics
Utah State University, Logan, UT 84322, USA
email: zhiqiang.wang@usu.edu
|
|---|
Return to the EJDE web page
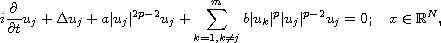
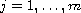 ,
,
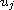 are complex-valued functions of
are complex-valued functions of
 ,
a,b are real numbers. It is shown that when
,
a,b are real numbers. It is shown that when
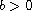 , and
, and
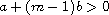 ,
for a certain range of p, traveling-wave solutions of this system exist,
and are orbitally stable.
,
for a certain range of p, traveling-wave solutions of this system exist,
and are orbitally stable.

