In this article we prove the existence of radial solutions with arbitrarily many sign changes for quasilinear Schrodinger equation
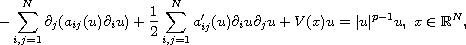
where
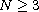 ,
,
 .
The proof is accomplished
by using minimization under a constraint.
.
The proof is accomplished
by using minimization under a constraint.
Gui Bao, Zhi-Qing Han
Abstract:
In this article we prove the existence of radial solutions with arbitrarily
many sign changes for quasilinear Schrodinger equation
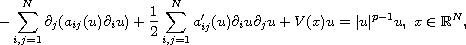
where
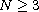 ,
,
 .
The proof is accomplished
by using minimization under a constraint.
.
The proof is accomplished
by using minimization under a constraint.
Submitted September 1, 2014. Published October 27, 2014.
Math Subject Classifications: 37J45, 58E05, 34C37,70H05.
Key Words: Quasilinear elliptic equations; variational methods; radial solutions.
Show me the PDF file (287 KB), TEX file for this article.
 |
Gui Bao School of Mathematics and Statistics Science Ludong University Yantai, Shandong 264025, China email: baoguigui@163.com |
|---|---|
 |
Zhiqing Han School of Mathematical Sciences Dalian University of Technology Dalian 116024, China email: hanzhiq@dlut.edu.cn |
Return to the EJDE web page