Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 238, pp. 1-13.
Patterns on surfaces of revolution in a diffusion problem with
variable diffusivity
Arnaldo Simal do Nascimento, Maicon Sonego
Abstract:
In this article we study the existence of non-constant stable stationary
solutions to the the diffusion equation
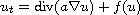 on a surface of revolution whose border is supplied with zero Neumann boundary
condition. Sufficient conditions on the geometry of the surface and on the
diffusivity function a are given for the existence of a function f
such the problem possesses such solutions.
on a surface of revolution whose border is supplied with zero Neumann boundary
condition. Sufficient conditions on the geometry of the surface and on the
diffusivity function a are given for the existence of a function f
such the problem possesses such solutions.
Submitted January 16, 2014. Published November 13, 2014.
Math Subject Classifications: 35K57, 35B36, 35R01, 35B25, 35B35, 34K20, 58J32.
Key Words: Patterns; diffusion; surface of revolution; stability.
Show me the PDF file (238 KB),
TEX file for this article.
 |
Arnaldo S. do Nascimento
Universidade Federal de São Carlos - D. M.
S. Carlos, S. P., Brasil
email: arnaldon@dm.ufscar.br
|
|---|
 |
Maicon Sônego
Universidade Federal de Itajubá - IMC
Itajubá, M. G. Brasil
email: mcn.sonego@unifei.edu.br
|
|---|
Return to the EJDE web page
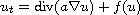 on a surface of revolution whose border is supplied with zero Neumann boundary
condition. Sufficient conditions on the geometry of the surface and on the
diffusivity function a are given for the existence of a function f
such the problem possesses such solutions.
on a surface of revolution whose border is supplied with zero Neumann boundary
condition. Sufficient conditions on the geometry of the surface and on the
diffusivity function a are given for the existence of a function f
such the problem possesses such solutions.
