Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 74, pp. 1-11.
Pullback attractor for non-autonomous p-Laplacian
equations with dynamic flux boundary conditions
Bo You, Fang Li
Abstract:
This article studies the long-time asymptotic behavior of solutions for
the non-autonomous
 -Laplacian equation
-Laplacian equation
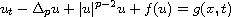
with dynamic flux boundary conditions
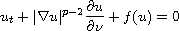
in a n-dimensional bounded smooth domain
 under some
suitable assumptions. We prove the existence of a pullback
attractor in
under some
suitable assumptions. We prove the existence of a pullback
attractor in
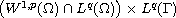 by asymptotic a priori estimate.
by asymptotic a priori estimate.
Submitted June 26, 2013. Published March 18, 2014.
Math Subject Classifications: 35B40, 37B55.
Key Words: Pullback attractor; Sobolev compactness embedding;
p-Laplacian; norm-to-weak continuous process;
asymptotic a priori estimate; non-autonomous;
nonlinear flux boundary conditions.
Show me the PDF file (251 KB),
TEX file for this article.
Bo You
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an, 710049, China
email: youb03@126.com
|
Fang Li
Department of Mathematics, Nanjing University
Nanjing, 210093, China
email: lifang101216@126.com
|
Return to the EJDE web page
 -Laplacian equation
-Laplacian equation
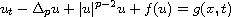
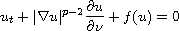
 under some
suitable assumptions. We prove the existence of a pullback
attractor in
under some
suitable assumptions. We prove the existence of a pullback
attractor in
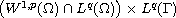 by asymptotic a priori estimate.
by asymptotic a priori estimate.