By applying the Laplace transform method, we prove that the linear differential equation

has the generalized Hyers-Ulam stability, where
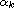 is
a scalar, y and f are n times continuously differentiable
and of exponential order.
is
a scalar, y and f are n times continuously differentiable
and of exponential order.
Qusuay H. Alqifiary, Soon-Mo Jung
Abstract:
By applying the Laplace transform method, we
prove that the linear differential equation

has the generalized Hyers-Ulam stability, where
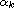 is
a scalar, y and f are n times continuously differentiable
and of exponential order.
is
a scalar, y and f are n times continuously differentiable
and of exponential order.
Submitted March 5, 2014. Published March 21, 2014.
Math Subject Classifications: 44A10, 39B82, 34A40, 26D10.
Key Words: Laplace transform method; differential equations;
generalized Hyers-Ulam stability.
Show me the PDF file (234 KB), TEX file for this article.
 |
Qusuay H. Alqifiary Department of Mathematics, University of Belgrade, Belgrade, Serbia. University of Al-Qadisiyah, Al-Diwaniya, Iraq email: qhaq2010@gmail.com |
|---|---|
 |
Soon-Mo Jung Mathematics Section College of Science and Technology Hongik University, 339--701 Sejong, Korea email: smjung@hongik.ac.kr |
Return to the EJDE web page