Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 08, pp. 1-14.
Existence and uniqueness for superlinear second-order differential
equations on the half-line
Imed Bachar, Habib Maagli
Abstract:
We prove the existence and uniqueness, and study the global behavior of
a positive continuous solution to the superlinear second-order differential
equation

where a,b are nonnegative constants such that a+b>0, A is a
continuous function on
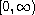 ,
positive and continuously
differentiable on
,
positive and continuously
differentiable on
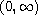 such that 1/A is integrable on
[0,1] and
such that 1/A is integrable on
[0,1] and
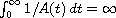 .
Here
.
Here
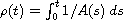 , for
, for
 and
g(t,s) is a nonnegative continuous function satisfying suitable
integrability condition. Our Approach is based on estimates of the Green's
function and a perturbation argument. Finally two illustrative examples are
given.
and
g(t,s) is a nonnegative continuous function satisfying suitable
integrability condition. Our Approach is based on estimates of the Green's
function and a perturbation argument. Finally two illustrative examples are
given.
Submitted October 11, 2014. Published January 5, 2015.
Math Subject Classifications: 34B15, 34B18, 34B27.
Key Words: Second order differential equation; boundary value problem;
half-line; Green's function; positive solution.
Show me the PDF file (256 KB),
TEX file for this article.
 |
Imed Bachar
King Saud University, College of Science
Mathematics Department, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: abachar@ksu.edu.sa
|
|---|
 |
Habib Mâagli
King Abdulaziz University, College of Sciences and Arts
Rabigh Campus, Department of Mathematics P.O. Box 344
Rabigh 21911, Saudi Arabia
email: habib.maagli@fst.rnu.tn, abobaker@kau.edu.sa
|
|---|
Return to the EJDE web page

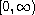 ,
positive and continuously
differentiable on
,
positive and continuously
differentiable on
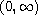 such that 1/A is integrable on
[0,1] and
such that 1/A is integrable on
[0,1] and
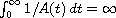 .
Here
.
Here
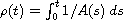 , for
, for
 and
g(t,s) is a nonnegative continuous function satisfying suitable
integrability condition. Our Approach is based on estimates of the Green's
function and a perturbation argument. Finally two illustrative examples are
given.
and
g(t,s) is a nonnegative continuous function satisfying suitable
integrability condition. Our Approach is based on estimates of the Green's
function and a perturbation argument. Finally two illustrative examples are
given.

