Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 142, pp. 1-11.
Orthogonal decomposition and asymptotic behavior for a
linear coupled system of Maxwell and heat equations
Celene Buriol, Marcio V. Ferreira
Abstract:
We study the asymptotic behavior in time of the solutions of a coupled
system of linear Maxwell equations with thermal effects.
We have two basic results. First, we prove the existence of a strong
solution and obtain the orthogonal decomposition of the electromagnetic field.
Also, choosing a suitable multiplier, we show that the total energy of
the system decays exponentially as
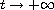 . The results obtained
for this linear problem can serve as a first attempt to study other nonlinear
problems related to this subject.
. The results obtained
for this linear problem can serve as a first attempt to study other nonlinear
problems related to this subject.
Submitted June 30, 2014. Published May 21, 2015.
Math Subject Classifications: 35Q61, 35Q79, 35B40.
Key Words: Maxwell equation; orthogonal decomposition; exponential decay.
Show me the PDF file (223 KB),
TEX file for this article.
 |
Celene Buriol
Department of Mathematics
Federal University of Santa Maria
Santa Maria, CEP 97105-900, RS, Brazil
email: celene@smail.ufsm.br
|
|---|
 |
Marcio V. Ferreira
Department of Mathematics
Federal University of Santa Maria
Santa Maria, CEP 97105-900, RS, Brazil
email: marcio.ferreira@ufsm.br
|
Return to the EJDE web page
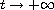 . The results obtained
for this linear problem can serve as a first attempt to study other nonlinear
problems related to this subject.
. The results obtained
for this linear problem can serve as a first attempt to study other nonlinear
problems related to this subject.

