Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 153, pp. 1-13.
Inverse coefficient problem for the semi-linear fractional telegraph equation
Halyna Lopushanska, Vitalia Rapita
Abstract:
We establish the unique solvability for an inverse problem for semi-linear
fractional telegraph equation
![$$
D^\alpha_t u+r(t)D^\beta_t u-\Delta u=F_0(x,t,u,D^\beta_t u), \quad
(x,t) \in \Omega_0\times (0,T]
$$](gifs/aa.gif)
with regularized fractional derivatives
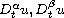 of orders
of orders
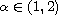 ,
,
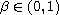 with respect to time on bounded cylindrical
domain. This problem consists in the determination of a pair of functions:
a classical solution
with respect to time on bounded cylindrical
domain. This problem consists in the determination of a pair of functions:
a classical solution
 of the first
boundary-value problem for such equation,
and an unknown continuous coefficient
of the first
boundary-value problem for such equation,
and an unknown continuous coefficient
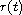 under the over-determination
condition
under the over-determination
condition
![$$
\int_{\Omega_0}u(x,t)\varphi(x)dx=F(t), \quad t\in [0,T]
$$](gifs/ag.gif)
with given functions
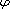 and
and
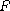 .
.
Submitted April 22, 2015. Published June 11, 2015.
Math Subject Classifications: 35S15.
Key Words: Fractional derivative; inverse boundary value problem;
over-determination integral condition; Green's function;
integral equation.
Show me the PDF file (261 KB),
TEX file for this article.
 |
Halyna Lopushanska
Department of Differential Equations
Ivan Franko National University of Lviv
Lviv, Ukraine
email: lhp@ukr.net
|
|---|
| |
Vitalia Rapita
Department of Differential Equations
Ivan Franko National University of Lviv
Lviv, Ukraine
email: vrapita@gmail.com
|
|---|
Return to the EJDE web page
![$$
D^\alpha_t u+r(t)D^\beta_t u-\Delta u=F_0(x,t,u,D^\beta_t u), \quad
(x,t) \in \Omega_0\times (0,T]
$$](gifs/aa.gif)
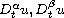 of orders
of orders
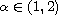 ,
,
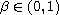 with respect to time on bounded cylindrical
domain. This problem consists in the determination of a pair of functions:
a classical solution
with respect to time on bounded cylindrical
domain. This problem consists in the determination of a pair of functions:
a classical solution
 of the first
boundary-value problem for such equation,
and an unknown continuous coefficient
of the first
boundary-value problem for such equation,
and an unknown continuous coefficient
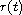 under the over-determination
condition
under the over-determination
condition
![$$
\int_{\Omega_0}u(x,t)\varphi(x)dx=F(t), \quad t\in [0,T]
$$](gifs/ag.gif)
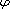 and
and
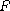 .
.
