We consider center conditions for plane polynomial systems of Abel type consisting of a linear center perturbed by the sum of 2 homogeneous polynomials of degrees n and 2n-1 where
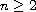 .
Using properties of Abel equations we obtain two general systems valid
for arbitrary values on n. For the cubic n=2 systems we find several
sets of new center conditions, some of which show that the results in a
paper by Hill, Lloyd and Pearson which were conjectured to be complete are
in fact not complete. We also present a particular system which appears to
be a counterexample to a conjecture by Zoladek et al. regarding
rational reversibility in cubic polynomial systems.
.
Using properties of Abel equations we obtain two general systems valid
for arbitrary values on n. For the cubic n=2 systems we find several
sets of new center conditions, some of which show that the results in a
paper by Hill, Lloyd and Pearson which were conjectured to be complete are
in fact not complete. We also present a particular system which appears to
be a counterexample to a conjecture by Zoladek et al. regarding
rational reversibility in cubic polynomial systems.
