Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 19, pp. 1-18.
Boundary behavior of solutions to a singular Dirichlet problem
with a nonlinear convection
Bo Li, Zhijun Zhang
Abstract:
In this article we analyze the exact boundary behavior of
solutions to the singular nonlinear Dirichlet problem
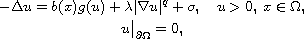
where
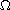 is a bounded domain with smooth
boundary in
is a bounded domain with smooth
boundary in
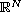 ,
,
![$q\in (0, 2]$](gifs/ad.gif) ,
,
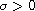 ,
,
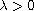 ,
,
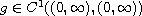 ,
,
 ,
,
 is decreasing on
is decreasing on
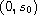 for some
for some
 ,
,
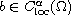 for some
for some
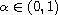 ,
is positive in
,
is positive in
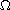 ,
but may be vanishing or
singular on the boundary. We show that
,
but may be vanishing or
singular on the boundary. We show that
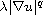 does not affect the first expansion of classical solutions near the
boundary.
does not affect the first expansion of classical solutions near the
boundary.
Submitted December 3, 2014. Published January 20, 2015.
Math Subject Classifications: 35J65, 35B05, 35J25, 60J50.
Key Words: Semilinear elliptic equation; singular Dirichlet problem;
nonlinear convection term; classical solution;
boundary behavior.
Show me the PDF file (305 KB),
TEX file for this article.
 |
Bo Li
School of mathematics and statistics
Lanzhou University
Lanzhou 730000, Gansu, China
email: libo_yt@163.com
|
|---|
 |
Zhijun Zhang
School of Mathematics and Information Science
Yantai University
Yantai 264005, Shandong, China
email: chinazjzhang2002@163.com, zhangzj@ytu.edu.cn
|
|---|
Return to the EJDE web page
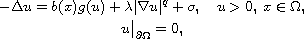
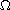 is a bounded domain with smooth
boundary in
is a bounded domain with smooth
boundary in
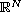 ,
,
![$q\in (0, 2]$](gifs/ad.gif) ,
,
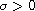 ,
,
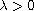 ,
,
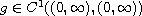 ,
,
 ,
,
 is decreasing on
is decreasing on
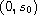 for some
for some
 ,
,
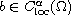 for some
for some
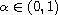 ,
is positive in
,
is positive in
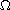 ,
but may be vanishing or
singular on the boundary. We show that
,
but may be vanishing or
singular on the boundary. We show that
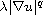 does not affect the first expansion of classical solutions near the
boundary.
does not affect the first expansion of classical solutions near the
boundary.

