Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 234, pp. 1-12.
Long-term behavior of a cyclic max-type system of difference equations
Tatjana Stevic, Bratislav Iricanin
Abstract:
We study the long-term behavior of positive solutions of the cyclic system of
difference equations
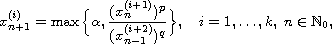
where
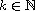 ,
,
 and where we
regard that
and where we
regard that
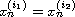 when
when
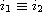 (mod
(mod
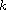 ).
We determine the set of parameters
).
We determine the set of parameters
 , p
and q in
, p
and q in
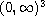 for which all such solutions are
bounded. In the other cases we show that the system has unbounded
solutions. For the case p=q we give some sufficient conditions
which guaranty the convergence of all positive solutions. The main
results in this paper generalize and complement some recent ones.
for which all such solutions are
bounded. In the other cases we show that the system has unbounded
solutions. For the case p=q we give some sufficient conditions
which guaranty the convergence of all positive solutions. The main
results in this paper generalize and complement some recent ones.
Submitted June 6 2015. Published September 11, 2015.
Math Subject Classifications: 39A10, 39A20.
Key Words: Max-type system of difference equations; cyclic system;
positive solutions; boundedness character; global attractivity.
Show me the PDF file (265 KB),
TEX file for this article.
| |
Tatjana Stevic
Faculty of Electrical Engineering
Belgrade University, Bulevar Kralja Aleksandra 73
11000 Beograd, Serbia
email: tanjas019@gmail.com
|
|---|
 |
Bratislav Iricanin
Faculty of Electrical Engineering
Belgrade University, Bulevar Kralja Aleksandra 73
11000 Beograd, Serbia
email: iricanin@etf.rs
|
|---|
Return to the EJDE web page
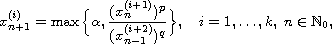
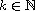 ,
,
 and where we
regard that
and where we
regard that
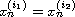 when
when
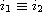 (mod
(mod
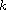 ).
We determine the set of parameters
).
We determine the set of parameters
 , p
and q in
, p
and q in
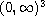 for which all such solutions are
bounded. In the other cases we show that the system has unbounded
solutions. For the case p=q we give some sufficient conditions
which guaranty the convergence of all positive solutions. The main
results in this paper generalize and complement some recent ones.
for which all such solutions are
bounded. In the other cases we show that the system has unbounded
solutions. For the case p=q we give some sufficient conditions
which guaranty the convergence of all positive solutions. The main
results in this paper generalize and complement some recent ones.
