Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 239, pp. 1-19.
Boundary controllability for a nonlinear beam equation
Xiao-Min Cao
Abstract:
This article concerns a nonlinear system modeling the bending vibrations
of a nonlinear beam of length
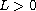 . First, we derive the existence of
long time solutions near an equilibrium. Then we prove that the nonlinear
beam is locally exact controllable around the equilibrium in
. First, we derive the existence of
long time solutions near an equilibrium. Then we prove that the nonlinear
beam is locally exact controllable around the equilibrium in
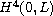 and with control functions in
and with control functions in
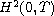 . The approach we used are open
mapping theorem, local controllability established by linearization,
and the induction.
. The approach we used are open
mapping theorem, local controllability established by linearization,
and the induction.
Submitted May 4, 2015. Published September 17, 2015.
Math Subject Classifications: 93B05, 35L75, 93C10, 93C20.
Key Words: Nonlinear beam equation; locally exact controllability;
equilibrium; smooth control.
Show me the PDF file (277 KB),
TEX file for this article.
 |
Xiao-Min Cao
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: caoxm@sxu.edu.cn
|
|---|
Return to the EJDE web page
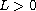 . First, we derive the existence of
long time solutions near an equilibrium. Then we prove that the nonlinear
beam is locally exact controllable around the equilibrium in
. First, we derive the existence of
long time solutions near an equilibrium. Then we prove that the nonlinear
beam is locally exact controllable around the equilibrium in
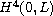 and with control functions in
and with control functions in
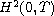 . The approach we used are open
mapping theorem, local controllability established by linearization,
and the induction.
. The approach we used are open
mapping theorem, local controllability established by linearization,
and the induction.
