Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 25, pp. 1-11.
Multiple solutions for fractional Schrodinger equations
Hongxia Shi, Haibo Chen
Abstract:
In this article we study the fractional Schr\"odinger equations
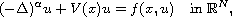
where
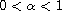 ,
,
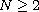 ,
,
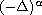 stands for the
fractional Laplacian of order
stands for the
fractional Laplacian of order
 .
First by using Morse theory in
combination with local linking arguments, we prove the existence of at least
two nontrivial solutions. Next we prove that the problem has k distinct
pairs of solutions by using the Clark theorem.
.
First by using Morse theory in
combination with local linking arguments, we prove the existence of at least
two nontrivial solutions. Next we prove that the problem has k distinct
pairs of solutions by using the Clark theorem.
Submitted November 16, 2014. Published January 27, 2015.
Math Subject Classifications: 35B38, 35G99.
Key Words: Fractional Schrodinger equations; variational methods;
Morse theory; local linking.
Show me the PDF file (244 KB),
TEX file for this article.
 |
Hongxia Shi
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: shihongxia5617@163.com
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: math_chb@163.com
|
|---|
Return to the EJDE web page
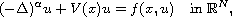
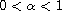 ,
,
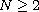 ,
,
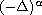 stands for the
fractional Laplacian of order
stands for the
fractional Laplacian of order
 .
First by using Morse theory in
combination with local linking arguments, we prove the existence of at least
two nontrivial solutions. Next we prove that the problem has k distinct
pairs of solutions by using the Clark theorem.
.
First by using Morse theory in
combination with local linking arguments, we prove the existence of at least
two nontrivial solutions. Next we prove that the problem has k distinct
pairs of solutions by using the Clark theorem.

