Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 278, pp. 1-9.
Basicity in Lp of root functions for differential equations
with involution
Leonid V. Kritskov, Abdizhahan M. Sarsenbi
Abstract:
We consider the differential equation
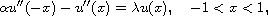
with the nonlocal boundary conditions
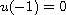 ,
,
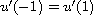 where
where
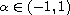 .
We prove that if
.
We prove that if
 is irrational then the system of its eigenfunctions is complete and minimal
in
is irrational then the system of its eigenfunctions is complete and minimal
in
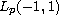 for any
for any
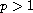 ,
but does not constitute a basis.
In the case of a rational value of r we specify the way of choosing
the associated functions which provides the system of all root functions
of the problem forms a basis in
,
but does not constitute a basis.
In the case of a rational value of r we specify the way of choosing
the associated functions which provides the system of all root functions
of the problem forms a basis in
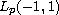 .
.
Submitted October 17, 2015. Published November 4, 2015.
Math Subject Classifications: 34K08, 34L10, 46B15.
Key Words: ODE with involution; nonlocal boundary-value problem;
basicity of root functions.
Show me the PDF file (235 KB),
TEX file for this article.
 |
Leonid V. Kritskov
Lomonosov Moscow State University
Faculty of Computational Mathematics and Cybernetics
119899 Moscow, Russia
email: kritskov@cs.msu.ru
|
|---|
 |
Abdizhahan M. Sarsenbi
Auezov South-Kazakhstan State University
Department of Mathematical Methods and Modeling
160012 Shymkent Kazakhstan
email: abzhahan@mail.ru
|
|---|
Return to the EJDE web page
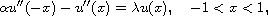
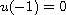 ,
,
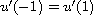 where
where
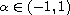 .
We prove that if
.
We prove that if
 is irrational then the system of its eigenfunctions is complete and minimal
in
is irrational then the system of its eigenfunctions is complete and minimal
in
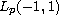 for any
for any
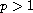 ,
but does not constitute a basis.
In the case of a rational value of r we specify the way of choosing
the associated functions which provides the system of all root functions
of the problem forms a basis in
,
but does not constitute a basis.
In the case of a rational value of r we specify the way of choosing
the associated functions which provides the system of all root functions
of the problem forms a basis in
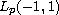 .
.

