Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 30, pp. 1-11.
Positive radially symmetric solution for a system of quasilinear
biharmonic equations in the plane
Joshua Barrow, Robert DeYeso III, Lingju Kong, Frank Petronella
Abstract:
We study the boundary value system for the two-dimensional quasilinear
biharmonic equations
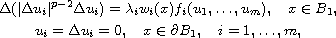
where
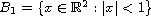 .
Under some suitable conditions on
.
Under some suitable conditions on
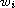 and
and
 ,
we discuss the existence,
uniqueness, and dependence of positive radially symmetric solutions on the
parameters
,
we discuss the existence,
uniqueness, and dependence of positive radially symmetric solutions on the
parameters
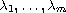 .
Moreover, two sequences are constructed so that they converge uniformly to
the unique solution of the problem.
An application to a special problem is also presented.
.
Moreover, two sequences are constructed so that they converge uniformly to
the unique solution of the problem.
An application to a special problem is also presented.
Submitted September 12, 2014. Published January 30, 2015.
Math Subject Classifications: 35J48, 35J92, 31A30.
Key Words: Positive radially symmetric solution; biharmonic equation;
uniqueness; dependence; cone; mixed monotone operator.
Show me the PDF file (248 KB),
TEX file for this article.
 |
Joshua Barrow
Department of Mathematics
Southern Adventist University
Collegedale, TN 37315, USA
email: joshuabarrow@southern.edu
|
|---|
 |
Robert DeYeso III
Department of Mathematics
University of Tennessee at Martin
Martin, TN 38238, USA
email: robldeye@ut.utm.edu
|
|---|
 |
Lingju Kong
Department of Mathematics
University of Tennessee at Chattanooga
Chattanooga, TN 37403, USA
email: Lingju-Kong@utc.edu
|
|---|
 |
Frank Petronella
Department of Mathematics
Baylor University
Waco, TX 76798, USA
email: Frank_Petronella@baylor.edu
|
|---|
Return to the EJDE web page
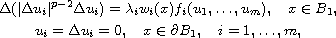
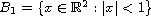 .
Under some suitable conditions on
.
Under some suitable conditions on
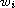 and
and
 ,
we discuss the existence,
uniqueness, and dependence of positive radially symmetric solutions on the
parameters
,
we discuss the existence,
uniqueness, and dependence of positive radially symmetric solutions on the
parameters
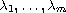 .
Moreover, two sequences are constructed so that they converge uniformly to
the unique solution of the problem.
An application to a special problem is also presented.
.
Moreover, two sequences are constructed so that they converge uniformly to
the unique solution of the problem.
An application to a special problem is also presented.



