In this article, we study the quenching behavior of solution to the semilinear heat equation
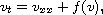
with
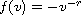 or
or
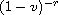 and
and

For this, we utilize the quenching problem
 with
with
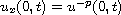 ,
,
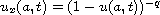 .
In the second problem, if
.
In the second problem, if
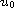 is an upper solution (a lower solution)
then we show that quenching occurs in a finite time, the
only quenching point is
is an upper solution (a lower solution)
then we show that quenching occurs in a finite time, the
only quenching point is
 (
(
 ) and
) and
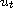 blows up at quenching
time. Further, we obtain a local solution by using positive steady
state. In the first problem, we first obtain a local solution by using
monotone iterations. Finally, for
blows up at quenching
time. Further, we obtain a local solution by using positive steady
state. In the first problem, we first obtain a local solution by using
monotone iterations. Finally, for
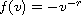 (
(
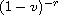 ), if
), if
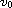 is an upper solution (a lower solution) then we show that quenching occurs
in a finite time, the only quenching point is
is an upper solution (a lower solution) then we show that quenching occurs
in a finite time, the only quenching point is
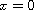 (
(
 ) and
) and
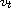 blows
up at quenching time.
blows
up at quenching time.