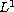 -data
-data
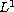 -data
-data
Alexander A. Kovalevsky, Francesco Nicolosi
Abstract:
In this article, we establish a sharp condition for the existence
of weak solutions to the Dirichlet problem for degenerate
nonlinear elliptic second-order equations with
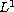 -data in a bounded
open set
-data in a bounded
open set
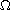 of
of
 with
with
 .
We assume that
.
We assume that
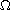 contains the origin and assume that
the growth and coercivity conditions on coefficients of the equations
involve the weighted function
contains the origin and assume that
the growth and coercivity conditions on coefficients of the equations
involve the weighted function
 ,
where
,
where
![$\alpha\in (0,1]$](gifs/af.gif) ,
and a parameter
,
and a parameter
 .
We prove that if
.
We prove that if
 ,
then the Dirichlet problem
has weak solutions for every
,
then the Dirichlet problem
has weak solutions for every
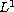 -right-hand side.
On the other hand, we find that if
-right-hand side.
On the other hand, we find that if
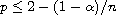 ,
then there exists an
,
then there exists an
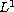 -datum
such that the corresponding Dirichlet problem
does not have weak solutions.
-datum
such that the corresponding Dirichlet problem
does not have weak solutions.
Submitted August 5, 2014. Published February 25, 2015.
Math Subject Classifications: 35J25, 35J60, 35J70, 35R05.
Key Words: Degenerate nonlinear elliptic second-order equation;
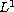 -data;
power weights; Dirichlet problem; weak solution;
existence and nonexistence of weak solutions.
-data;
power weights; Dirichlet problem; weak solution;
existence and nonexistence of weak solutions.
Show me the PDF file (256 KB), TEX file for this article.
 |
Alexander A. Kovalevsky Department of Equations of Mathematical Physics Krasovsky Institute of Mathematics and Mechanics Ural Branch of Russian Academy of Sciences Ekaterinburg, Russia email: alexkvl71@mail.ru |
|---|---|
 |
Francesco Nicolosi Department of Mathematics and Informatics University of Catania Catania, Italy email: fnicolosi@dmi.unict.it |
Return to the EJDE web page