Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 63, pp. 1-23.
Existence of solutions for a variable exponent system without PS conditions
Li Yin, Yuan Liang, Qihu Zhang, Chunshan Zhao
Abstract:
In this article, we study the existence of solution for the following elliptic
system of variable exponents with perturbation terms
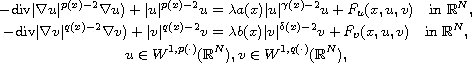
where the corresponding functional does not satisfy PS conditions.
We obtain a sufficient condition for the existence of solution and
also present a result on asymptotic behavior of solutions at infinity.
Submitted September 29, 2014. Published March 13, 2015.
Math Subject Classifications: 35J47.
Key Words: Variable exponent system; integral functional;
PS condition; variable exponent Sobolev space.
Show me the PDF file (336 KB),
TEX file for this article.
 |
Li Yin
College of Information and Management Science
Henan Agricultural University
Zhengzhou, Henan 450002, China
email: mathsr@163.com
|
|---|
 |
Yuan Liang
Junior College, Zhejiang Wanli University
Ningbo, Zhejiang 315100, China
email: ly0432@163.com
|
|---|
 |
Qihu Zhang
College of Mathematics and Information Science
Zhengzhou University of Light Industry
Zhengzhou, Henan 450002, China
email: zhangqihu@yahoo.com, zhangqh1999@yahoo.com.cn
|
|---|
 |
Chunshan Zhao
Department of Mathematical Sciences
Georgia Southern University
Statesboro, GA 30460, USA
email: czhao@GeorgiaSouthern.edu
|
|---|
Return to the EJDE web page