Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 91, pp. 1-9.
Existence of solutions to quasilinear Schrodinger equations
with indefinite potential
Zupei Shen, Zhiqing Han
Abstract:
In this article, we study the existence and multiplicity of solutions
of the quasilinear Schrodinger equation
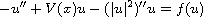
on
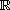 ,
where the potential
,
where the potential
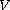 allows sign changing and the
nonlinearity satisfies conditions weaker than the classical
Ambrosetti-Rabinowitz condition. By a local linking theorem and the fountain
theorem, we obtain the existence and multiplicity of solutions for the equation.
allows sign changing and the
nonlinearity satisfies conditions weaker than the classical
Ambrosetti-Rabinowitz condition. By a local linking theorem and the fountain
theorem, we obtain the existence and multiplicity of solutions for the equation.
Submitted October 24, 2014. Published April 10, 2015.
Math Subject Classifications: 37J45, 58E05, 34C37, 70H05.
Key Words: Quasilinear Schrodinger equation; local linking;
fountain theorem; indefinite potential.
Show me the PDF file (217 KB),
TEX file for this article.
 |
Zupei Shen
School of Mathematical Sciences
Dalian University of Technology
Dalian 116024, China
email: pershen@mail.dlut.edu.cn
|
|---|
 |
Zhiqing Han
School of Mathematical Sciences
Dalian University of Technology
Dalian 116024, China
email: hanzhiq@dlut.edu.cn Phone(Fax) +86 41184707268
|
|---|
Return to the EJDE web page
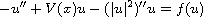
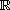 ,
where the potential
,
where the potential
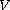 allows sign changing and the
nonlinearity satisfies conditions weaker than the classical
Ambrosetti-Rabinowitz condition. By a local linking theorem and the fountain
theorem, we obtain the existence and multiplicity of solutions for the equation.
allows sign changing and the
nonlinearity satisfies conditions weaker than the classical
Ambrosetti-Rabinowitz condition. By a local linking theorem and the fountain
theorem, we obtain the existence and multiplicity of solutions for the equation.

