Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 108, pp. 1-15.
Superlinear singular fractional boundary-value problems
Imed Bachar, Habib Maagli
Abstract:
In this article, we study the superlinear fractional
boundary-value problem
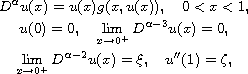
where
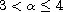 ,
,
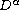 is the Riemann-Liouville
fractional derivative and
is the Riemann-Liouville
fractional derivative and
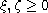 are such that
are such that
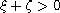 .
The function
.
The function
 that may be singular at x=0 and x=1 is required to satisfy
convenient hypotheses to be stated later.
By means of a perturbation argument, we establish the existence,
uniqueness and global asymptotic behavior of a positive continuous solution
to the above problem.An example is given to illustrate our main results.
that may be singular at x=0 and x=1 is required to satisfy
convenient hypotheses to be stated later.
By means of a perturbation argument, we establish the existence,
uniqueness and global asymptotic behavior of a positive continuous solution
to the above problem.An example is given to illustrate our main results.
Submitted February 8, 2016. Published April 26, 2016.
Math Subject Classifications: 34A08, 34B15, 34B18, 34B27.
Key Words: Fractional differential equation; positive solution;
Green's function; perturbation arguments.
Show me the PDF file (267 KB),
TEX file, and other files for this article.
 |
Imed Bachar
King Saud University, College of Science
Mathematics Department, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: abachar@ksu.edu.sa
|
|---|
 |
Habib Mâagli
King Abdulaziz University, Rabigh Campus
College of Sciences and Arts, Department of Mathematics
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: abobaker@kau.edu.sa, habib.maagli@fst.rnu.tn
|
|---|
Return to the EJDE web page
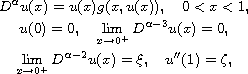
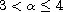 ,
,
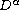 is the Riemann-Liouville
fractional derivative and
is the Riemann-Liouville
fractional derivative and
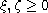 are such that
are such that
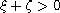 .
The function
.
The function
 that may be singular at x=0 and x=1 is required to satisfy
convenient hypotheses to be stated later.
By means of a perturbation argument, we establish the existence,
uniqueness and global asymptotic behavior of a positive continuous solution
to the above problem.An example is given to illustrate our main results.
that may be singular at x=0 and x=1 is required to satisfy
convenient hypotheses to be stated later.
By means of a perturbation argument, we establish the existence,
uniqueness and global asymptotic behavior of a positive continuous solution
to the above problem.An example is given to illustrate our main results.

