In this article we prove the existence of an infinite number of radial solutions of
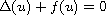with prescribed number of zeros on the exterior of
the ball of radius R>0 centered at the origin in
where f is odd with f<0 on
,
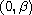f>0 on
where
.
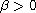Janak Joshi, Joseph Iaia
Abstract:
In this article we prove the existence of an infinite number of radial solutions
of
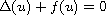with prescribed number of zeros on the exterior of
the ball of radius R>0 centered at the origin in
where f is odd with f<0 on
,
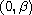f>0 on
where
.
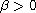Submitted December 31, 2015. Published May 3, 2016.
Math Subject Classifications: 34B40, 35B05.
Key Words: Exterior domains; semilinear; superlinear; radial.
Show me the PDF file (227 KB), TEX file for this article.
 |
Janak Joshi Department of Mathematics University of North Texas, P.O. Box 311430 Denton, TX 76203-1430, USA email: janakrajjoshi@my.unt.edu |
|---|---|
 |
Joseph Iaia Department of Mathematics University of North Texas, P.O. Box 311430 Denton, TX 76203-1430, USA email: iaia@unt.edu |
Return to the EJDE web page