In this article, we apply the Nehari manifold to prove the existence of a solution of the fractional differential equation
![$$\displaylines{
\frac{d}{dt} \Big(\frac12 {\,}_0D_t^{-\beta}(u'(t))
+\frac12 {\,}_tD_T^{-\beta}(u'(t)))= f(t,u(t))
+ \lambda h(t)|u(t)|^{r-2}u(t), \cr
\text{a.e } t\in [0,T],\cr
u(0)=u(T)=0,
}$$](gifs/aa.gif)
where
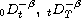are the left and right
Riemann-Liouville fractional integrals, respectively, of order
.
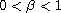Khaled Ben Ali, Abdeljabbar Ghanmi, Khaled Kefi
Abstract:
In this article, we apply the Nehari manifold to prove the existence
of a solution of the fractional differential equation
where
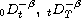are the left and right
Riemann-Liouville fractional integrals, respectively, of order
.
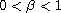Submitted January 28, 2016. Published May 10, 2016.
Math Subject Classifications: 26A33, 58E05, 35J60.
Key Words: Fractional differential equation; left and right fractional derivatives;
boundary value problem; Nehari manifold.
Show me the PDF file (234 KB), TEX file for this article.
 |
Khaled Ben Ali Département de Mathématiques Faculté des Sciences de Tunis Campus Universitaire, 2092 Tunis, Tunisia email: benali.khaled@yahoo.fr |
|---|---|
 |
Abdeljabbar Ghanmi Department of Mathematics Faculty of Sciences and Arts Khulais, University of Jeddah, Saudi Arabia email: Abdeljabbar.ghanmi@lamsin.rnu.tn |
 |
Khaled Kefi Département de Mathématiques Faculté des Sciences de Tunis Campus Universitaire, 2092 Tunis, Tunisia email: khaled_kefi@yahoo.fr |
Return to the EJDE web page