Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 135, pp. 1-16.
Multiple sign-changing solutions for Kirchhoff type problems
Cyril Joel Batkam
Abstract:
This article concerns the existence of sign-changing solutions
to nonlocal Kirchhoff type problems of the form
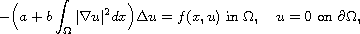
where
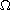 is a bounded domain in
is a bounded domain in
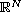 (
(
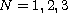 )
with smooth boundary,
)
with smooth boundary,
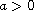 ,
,
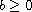 ,
and
,
and
 is a continuous function.
We first establish a new sign-changing version of the symmetric mountain
pass theorem and then apply it to prove the existence of a sequence of
sign-changing solutions with higher and higher energy.
is a continuous function.
We first establish a new sign-changing version of the symmetric mountain
pass theorem and then apply it to prove the existence of a sequence of
sign-changing solutions with higher and higher energy.
Submitted December 17, 2015. Published June 7, 2016.
Math Subject Classifications: 35J60, 35A15, 35J20, 35J25.
Key Words: Kirchhoff type equation; sign-changing solution;
multiple solutions; critical point theorem.
Show me the PDF file (285 KB),
TEX file for this article.
 |
Cyril Joel Batkam
HEC Montreal
3000 Chemin de la Cate-Sainte-Catherine
Montrel, QC, H3T 2B1, Canada
email: cyril-joel.batkam@hec.ca, cyril.joel.batkam@usherbrooke.ca
|
|---|
Return to the EJDE web page
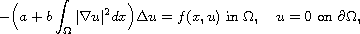
 is a bounded domain in
is a bounded domain in
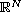 (
(
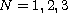 )
with smooth boundary,
)
with smooth boundary,
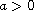 ,
,
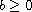 ,
and
,
and
 is a continuous function.
We first establish a new sign-changing version of the symmetric mountain
pass theorem and then apply it to prove the existence of a sequence of
sign-changing solutions with higher and higher energy.
is a continuous function.
We first establish a new sign-changing version of the symmetric mountain
pass theorem and then apply it to prove the existence of a sequence of
sign-changing solutions with higher and higher energy.
