Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 180, pp. 1-7.
Multiple positive solutions for Dirichlet problem of prescribed
mean curvature equations in Minkowski spaces
Ruyun Ma, Tianlan Chen
Abstract:
In this article, we consider the Dirichlet problem for the prescribed
mean curvature equation in the Minkowski space,
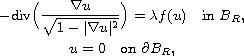
where
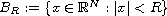 ,
,
 is a parameter and
is a parameter and
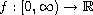 is continuous. We apply
some standard variational techniques to show how changes in the sign of
f lead to multiple positive solutions of the above problem for
sufficiently large
is continuous. We apply
some standard variational techniques to show how changes in the sign of
f lead to multiple positive solutions of the above problem for
sufficiently large
 .
.
Submitted June 3, 2016. Published July 7, 2016.
Math Subject Classifications: 35B15, 34K28, 34L30, 35J60, 35J65.
Key Words: Dirichlet problem; Minkowski-curvature;
positive solutions; variational methods.
Show me the PDF file (206 KB),
TEX file for this article.
 |
Ruyun Ma
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: mary@nwnu.edu.cn
|
|---|
 |
Tianlan Chen
Northwest Normal University
Lanzhou 730070, China
email: chentianlan511@126.com
|
|---|
Return to the EJDE web page
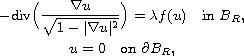
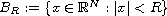 ,
,
 is a parameter and
is a parameter and
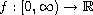 is continuous. We apply
some standard variational techniques to show how changes in the sign of
f lead to multiple positive solutions of the above problem for
sufficiently large
is continuous. We apply
some standard variational techniques to show how changes in the sign of
f lead to multiple positive solutions of the above problem for
sufficiently large
 .
.

