Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 203, pp. 1-9.
Bifurcation and multiplicity of solutions for the fractional Laplacian with
critical exponential nonlinearity
Pawan Kumar Mishra, Konijeti Sreenadh
Abstract:
We study the fractional elliptic equation
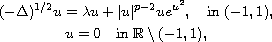
where
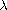 is a positive real parameter, p>2 and
is a positive real parameter, p>2 and
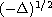 is the fractional Laplacian operator. We show the multiplicity of solutions
for this problem using an abstract critical point theorem of literature
in critical point theory. Precisely, we extended the result of
Cerami, Fortuno and Struwe [5] for the fractional Laplacian with
exponential nonlinearity.
is the fractional Laplacian operator. We show the multiplicity of solutions
for this problem using an abstract critical point theorem of literature
in critical point theory. Precisely, we extended the result of
Cerami, Fortuno and Struwe [5] for the fractional Laplacian with
exponential nonlinearity.
Submitted March 5, 2016. Published July 27, 2016.
Math Subject Classifications: 35A15, 35R11
Key Words: Fractional Laplacian; bifurcation; exponential growth.
Show me the PDF file (228 KB),
TEX file for this article.
 |
Pawan Kumar Mishra
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: pawanmishra31284@gmail.com
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: sreenadh@gmail.com
|
|---|
Return to the EJDE web page
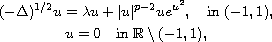
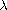 is a positive real parameter, p>2 and
is a positive real parameter, p>2 and
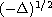 is the fractional Laplacian operator. We show the multiplicity of solutions
for this problem using an abstract critical point theorem of literature
in critical point theory. Precisely, we extended the result of
Cerami, Fortuno and Struwe [5] for the fractional Laplacian with
exponential nonlinearity.
is the fractional Laplacian operator. We show the multiplicity of solutions
for this problem using an abstract critical point theorem of literature
in critical point theory. Precisely, we extended the result of
Cerami, Fortuno and Struwe [5] for the fractional Laplacian with
exponential nonlinearity.

