In this work we study the existence and multiplicity result of solutions to the equation

where
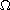 is a bounded smooth domain of
is a bounded smooth domain of
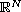 ,
,
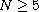 ,
,
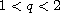 or
or
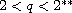 ,
,
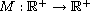 is a continuous function. Since there is a competition between the
function M and the critical exponent, we need to make a truncation on
the function M. This truncation allows to define an auxiliary problem.
We show that, for
is a continuous function. Since there is a competition between the
function M and the critical exponent, we need to make a truncation on
the function M. This truncation allows to define an auxiliary problem.
We show that, for
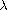 large, exists one solution and for
large, exists one solution and for
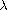 small there are infinitely many solutions for the auxiliary problem.
Here we use arguments due to Brezis-Niremberg [12] to show
the existence result and genus theory due to Krasnolselskii [29] to
show the multiplicity result. Using the size of
small there are infinitely many solutions for the auxiliary problem.
Here we use arguments due to Brezis-Niremberg [12] to show
the existence result and genus theory due to Krasnolselskii [29] to
show the multiplicity result. Using the size of
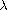 ,
we show that
each solution of the auxiliary problem is a solution of the original problem.
,
we show that
each solution of the auxiliary problem is a solution of the original problem.

