Electron. J. Differential Equations,
Vol. 2016 (2016), No. 231, pp. 1-9.
Positive solutions of multi-point boundary value problems
Youyuan Yang, Qiru Wang
Abstract:
This article concerns the boundary value problem consisting of the
nonlinear differential equation
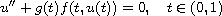
and the multi-point boundary conditions
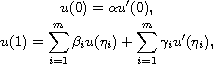
where
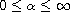 ,
,
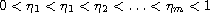 ,
,
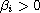 ,
,
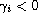 (
(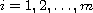 ).
By using the fixed point index theory, we establish the existences of at
least one positive solution and at least two positive solutions.
).
By using the fixed point index theory, we establish the existences of at
least one positive solution and at least two positive solutions.
Submitted December 30, 2015. Published August 24, 2016.
Math Subject Classifications: 34B10, 34B18.
Key Words: Boundary value problems; multi-point boundary conditions;
second-order nonlinear differential equations;
positive solutions; fixed point index.
An addendum was posted on February 7, 2017. It points out some mistakes in this
article; see the last page.
Show me the PDF file (216 KB),
TEX file for this article.
 |
Youyuan Yang
School of Mathematics
Sun Yat-Sen University
Guangzhou 510275, China
email: yangyouyuan2016@163.com
|
|---|
 |
Qiru Wang
School of Mathematics
Sun Yat-Sen University
Guangzhou 510275, China
email: mcswqr@mail.sysu.edu.cn
|
|---|
Return to the EJDE web page
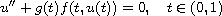
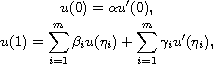
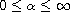 ,
,
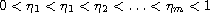 ,
,
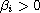 ,
,
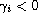 (
(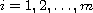 ).
By using the fixed point index theory, we establish the existences of at
least one positive solution and at least two positive solutions.
).
By using the fixed point index theory, we establish the existences of at
least one positive solution and at least two positive solutions.

