Electron. J. Differential Equations,
Vol. 2016 (2016), No. 242, pp. 1-11.
Stability for noncoercive elliptic equations
Shuibo Huang, Qiaoyu Tian, Jie Wang, Jia Mu
Abstract:
In this article, we consider the stability for elliptic problems
that have degenerate coercivity in their principal part,
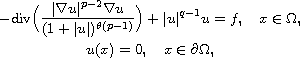
where
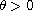 ,
,
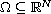 is a bounded domain.
Let K be a compact subset in
is a bounded domain.
Let K be a compact subset in
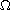 with zero r-capacity (
with zero r-capacity (
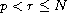 ).
We prove that if
).
We prove that if
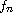 is a sequence of functions which converges strongly
to f in
is a sequence of functions which converges strongly
to f in
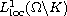 and
and
![$q>r(p-1)[1+\theta(p-1)]/(r-p)$](gifs/ah.gif) , and
, and
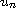 is the sequence of solutions
of the corresponding problems with datum
is the sequence of solutions
of the corresponding problems with datum
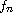 .
Then
.
Then
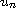 converges to the solution u.
converges to the solution u.
Submitted April 29, 2016. Published September 5, 2016.
Math Subject Classifications: 37K45,35J60.
Key Words: Removable singularity; capacity; noncoercive elliptic equation.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Shuibo Huang
School of Mathematics and Computer
Northwest University for Nationalities
Lanzhou, Gansu 730000, China
email: huangshuibo2008@163.com
|
|---|
 |
Qiaoyu Tian
School of Mathematics and Computer
Northwest University for Nationalities
Lanzhou, Gansu 730000, China
email: tianqiaoyu2004@163.com
|
|---|
 |
Jie Wang
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu 730050, China
email: jiema138@163.com
|
|---|
 |
Jia Mu
School of Mathematics and Computer
Northwest University for Nationalities
Lanzhou, Gansu 730000, China
email: mujia88@163.com
|
|---|
Return to the EJDE web page
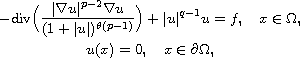
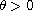 ,
,
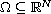 is a bounded domain.
Let K be a compact subset in
is a bounded domain.
Let K be a compact subset in
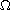 with zero r-capacity (
with zero r-capacity (
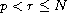 ).
We prove that if
).
We prove that if
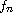 is a sequence of functions which converges strongly
to f in
is a sequence of functions which converges strongly
to f in
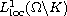 and
and
![$q>r(p-1)[1+\theta(p-1)]/(r-p)$](gifs/ah.gif) , and
, and
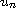 is the sequence of solutions
of the corresponding problems with datum
is the sequence of solutions
of the corresponding problems with datum
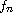 .
Then
.
Then
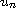 converges to the solution u.
converges to the solution u.



