Electron. J. Differential Equations,
Vol. 2016 (2016), No. 251, pp. 1-17.
Positive solutions for a second-order Phi-Laplacian equations
with limiting nonlocal boundary conditions
George L. Karakostas, Konstantina G. Palaska, Panagiotis Ch. Tsamatos
Abstract:
Motivated, mainly, by the works of Fewster-Young and Tisdell [9,10]
and Orpel [30], as well as the papers by Karakostas [21,22,23],
we give sufficient conditions to guarantee the existence of (nontrivial)
solutions of the second-order Phi-Laplacian equation
![$$
\frac{1}{p(t)}\frac{d}{dt}[p(t)\Phi(u'(t))]+(Fu)(t)=0,\quad\text{a.e. }
t\in[0,1]=:I,
$$](gifs/aa.gif)
which satisfy the nonlocal boundary value conditions of the
limiting Sturm-Liouville form
![$$
\lim_{t\to 0}[p(t)\Phi(u'(t))]=\int_0^1u(s)d\eta(s),\quad
\lim_{t\to 1}[p(t)\Phi(u'(t))]=-\int_0^1u(s)d\zeta(s).
$$](gifs/ab.gif)
Here
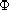 is an increasing homeomorphism of the real line onto itself
and F is an operator acting on the function u and on its first
derivative with the characteristic property that
is an increasing homeomorphism of the real line onto itself
and F is an operator acting on the function u and on its first
derivative with the characteristic property that
 is a
is a
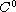 -type, or
-type, or
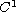 -type
Caratheodory operator, a meaning introduced here.
Examples are given to illustrate both cases.
-type
Caratheodory operator, a meaning introduced here.
Examples are given to illustrate both cases.
Submitted April 19, 2016. Published September 20, 2016.
Math Subject Classifications: 34B18, 34B10.
Key Words: Positive solution; Sturm-Liouville equation; Phi-Laplacian;
Schauder's fixed point theorem.
Show me the PDF file (275 KB),
TEX file for this article.
 |
George L. Karakostas
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: gkarako@uoi.gr, gkarako@hotmail.com
|
|---|
 |
Konstantina G. Palaska
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: cpalaska@cc.uoi.gr
|
|---|
 |
Panagiotis Ch. Tsamatos
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: ptsamato@cc.uoi.gr
|
|---|
Return to the EJDE web page
![$$
\frac{1}{p(t)}\frac{d}{dt}[p(t)\Phi(u'(t))]+(Fu)(t)=0,\quad\text{a.e. }
t\in[0,1]=:I,
$$](gifs/aa.gif)
![$$
\lim_{t\to 0}[p(t)\Phi(u'(t))]=\int_0^1u(s)d\eta(s),\quad
\lim_{t\to 1}[p(t)\Phi(u'(t))]=-\int_0^1u(s)d\zeta(s).
$$](gifs/ab.gif)
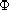 is an increasing homeomorphism of the real line onto itself
and F is an operator acting on the function u and on its first
derivative with the characteristic property that
is an increasing homeomorphism of the real line onto itself
and F is an operator acting on the function u and on its first
derivative with the characteristic property that
 is a
is a
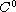 -type, or
-type, or
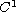 -type
Caratheodory operator, a meaning introduced here.
Examples are given to illustrate both cases.
-type
Caratheodory operator, a meaning introduced here.
Examples are given to illustrate both cases.


