We study the asymptotic behavior of eventually positive solutions of the second-order half-linear differential equation
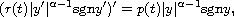
where r(t) and p(t) are positive continuous functions on
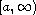 ,
,
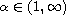 .
The aim of this article is
twofold. On the one hand, we show applications of a wide variety
of tools, like the Karamata theory of regular variation, the de
Haan theory, the Riccati technique, comparison theorems, the
reciprocity principle, a certain transformation of dependent
variable, and principal solutions. On the other hand, we solve
open problems posed in the literature and generalize existing
results. Most of our observations are new also in the linear
case.
.
The aim of this article is
twofold. On the one hand, we show applications of a wide variety
of tools, like the Karamata theory of regular variation, the de
Haan theory, the Riccati technique, comparison theorems, the
reciprocity principle, a certain transformation of dependent
variable, and principal solutions. On the other hand, we solve
open problems posed in the literature and generalize existing
results. Most of our observations are new also in the linear
case.
