In this article, we analyze the blow-up rate of the unique solution to the singular boundary value problem
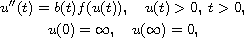
where f(u) grows more slowly than
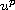 (p > 1) at infinity,
and
(p > 1) at infinity,
and
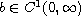 which is positive and non-decreasing
(it may vanish at zero).
which is positive and non-decreasing
(it may vanish at zero).
Ling Mi
Abstract:
In this article, we analyze the blow-up rate of the unique
solution to the singular boundary value problem
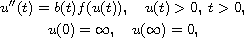
where f(u) grows more slowly than
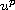 (p > 1) at infinity,
and
(p > 1) at infinity,
and
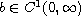 which is positive and non-decreasing
(it may vanish at zero).
which is positive and non-decreasing
(it may vanish at zero).
Submitted June 30, 2015. Published November 30, 2016.
Math Subject Classifications: 35J25, 35J60, 35J65.
Key Words: One-dimensional problems; uniqueness of the solution;
boundary behavior.
Show me the PDF file (244 KB), TEX file for this article.
 |
Ling Mi School of Science Linyi University Linyi, Shandong 276005, China email: mi-ling@163.com |
|---|
Return to the EJDE web page