Electron. J. Differential Equations,
Vol. 2016 (2016), No. 336, pp. 1-9.
Existence of positive symmetric solutions for an integral
boundary-value problem with phi-Laplacian operator
Yonghong Ding
Abstract:
In this article, we show the existence of three positive symmetric
solutions for the integral boundary-value problem with
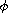 -Laplacian
-Laplacian
![$$\displaylines{
(\phi(u'(t)))'+f(t,u(t),u'(t))=0,\quad t\in[0,1],\cr
u(0)=u(1)=\int_0^1u(r)g(r)\,dr,
}$$](gifs/ab.gif)
where
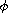 is an odd, increasing homeomorphism from
is an odd, increasing homeomorphism from
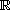 onto
onto
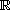 .
Our main tool is a fixed point theorem due to
Avery and Peterson. An example shows an applications of the obtained results.
.
Our main tool is a fixed point theorem due to
Avery and Peterson. An example shows an applications of the obtained results.
Submitted May 18, 2016. Published December 28, 2016.
Math Subject Classifications: 34B15, 34B18.
Key Words: phi-Laplacian; fixed point; cone; positive symmetric solutions.
Show me the PDF file (211 KB),
TEX file for this article.
 |
Yonghong Ding
Department of Mathematics
Tianshui Normal University
Tianshui 741000, China
email: dyh198510@126.com
|
|---|
Return to the EJDE web page
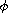 -Laplacian
-Laplacian
![$$\displaylines{
(\phi(u'(t)))'+f(t,u(t),u'(t))=0,\quad t\in[0,1],\cr
u(0)=u(1)=\int_0^1u(r)g(r)\,dr,
}$$](gifs/ab.gif)
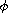 is an odd, increasing homeomorphism from
is an odd, increasing homeomorphism from
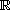 onto
onto
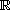 .
Our main tool is a fixed point theorem due to
Avery and Peterson. An example shows an applications of the obtained results.
.
Our main tool is a fixed point theorem due to
Avery and Peterson. An example shows an applications of the obtained results.
