Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 81, pp. 1-13.
Reaction diffusion equations with boundary degeneracy
Huashui Zhan
Abstract:
In this article, we consider the reaction diffusion equation
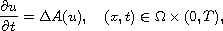
with the homogeneous boundary condition. Inspired by the Fichera-Oleinik
theory, if the equation is not only strongly degenerate in the interior
of
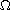 , but also degenerate on the boundary, we show that the solution
of the equation is free from any limitation of the boundary condition.
, but also degenerate on the boundary, we show that the solution
of the equation is free from any limitation of the boundary condition.
Submitted May 14, 2015. Published March 23, 2016.
Math Subject Classifications: 35L65, 35K85, 35R35.
Key Words: Reaction diffusion equation; Fichera-Oleinik theory;
boundary condition; degeneracy.
Show me the PDF file (257 KB),
TEX file for this article.
 |
Huashui Zhan
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: 2012111007@xmut.edu.cn
|
|---|
Return to the EJDE web page
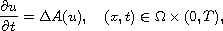
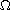 , but also degenerate on the boundary, we show that the solution
of the equation is free from any limitation of the boundary condition.
, but also degenerate on the boundary, we show that the solution
of the equation is free from any limitation of the boundary condition.
