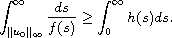Electron. J. Differential Equations,
Vol. 2017 (2017), No. 116, pp. 1-10.
Instantaneous blow-up of semilinear
non-autonomous equations with fractional diffusion
Jose Villa-Morales
Abstract:
We consider the Cauchy initial value problem
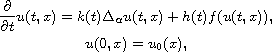
where
 is the fractional Laplacian for
is the fractional Laplacian for
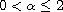 .
We prove that if the initial condition
.
We prove that if the initial condition
 is non-negative,
bounded and measurable then the problem has a global integral solution
when the source term f is non-negative, locally Lipschitz and satisfies the
generalized Osgood's condition
is non-negative,
bounded and measurable then the problem has a global integral solution
when the source term f is non-negative, locally Lipschitz and satisfies the
generalized Osgood's condition
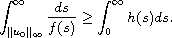
Also, we prove that if the initial data is unbounded then the
generalized Osgood's condition does not guarantee the existence of
a global solution. It is important to point out that the proof of the
existence hinges on the role of the function h. Analogously, the
function k plays a central role in the proof of the instantaneous blow-up.
Submitted September 5, 2016. Published May 2, 2017.
Math Subject Classifications: 35K05, 45K05, 60G52, 34G20.
Key Words: Generalized Osgood's condition; semilinear equations;
fractional diffusion; instantaneous blow-up.
Show me the PDF file (239 KB),
TEX file for this article.
 |
José Villa-Morales
Departamento de Matemáticas y Física
Universidad Autónoma de Aguascalientes
Av. Universidad No. 940, Cd. Universitaria
Aguascalientes, Ags., C.P. 20131, Mexico
email: jvilla@correo.uaa.mx
|
Return to the EJDE web page
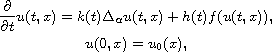
 is the fractional Laplacian for
is the fractional Laplacian for
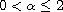 .
We prove that if the initial condition
.
We prove that if the initial condition
 is non-negative,
bounded and measurable then the problem has a global integral solution
when the source term f is non-negative, locally Lipschitz and satisfies the
generalized Osgood's condition
is non-negative,
bounded and measurable then the problem has a global integral solution
when the source term f is non-negative, locally Lipschitz and satisfies the
generalized Osgood's condition