Electron. J. Differential Equations,
Vol. 2017 (2017), No. 132, pp. 1-10.
Existence and nonexistence of solutions for sublinear
problems with prescribed number of zeros on exterior domains
Janak Joshi
Abstract:
We prove existence of radial solutions of
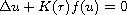 on the
exterior of the ball, of radius R, centered at the origin in
on the
exterior of the ball, of radius R, centered at the origin in
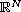 such that
such that
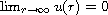 if R>0 is sufficiently small.
We assume
if R>0 is sufficiently small.
We assume
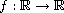 is odd and there exists a
is odd and there exists a
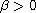 with f<0 on
with f<0 on
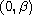 ,
f>0 on
,
f>0 on
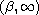 with f sublinear
for large u, and
with f sublinear
for large u, and
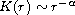 for large r with
for large r with
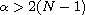 .
We also prove nonexistence if R>0 is sufficiently large.
.
We also prove nonexistence if R>0 is sufficiently large.
Submitted March 6, 2017. Published May 16, 2017.
Math Subject Classifications: 34B40, 35B05.
Key Words: Exterior domain; sublinear; radial solution.
Show me the PDF file (237 KB),
TEX file for this article.
 |
Janak Joshi
Department of Mathematics
University of North Texas
Denton, TX 76203, USA
email: janakrajjoshi@my.unt.edu
|
|---|
Return to the EJDE web page
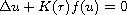 on the
exterior of the ball, of radius R, centered at the origin in
on the
exterior of the ball, of radius R, centered at the origin in
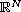 such that
such that
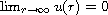 if R>0 is sufficiently small.
We assume
if R>0 is sufficiently small.
We assume
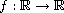 is odd and there exists a
is odd and there exists a
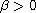 with f<0 on
with f<0 on
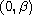 ,
f>0 on
,
f>0 on
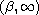 with f sublinear
for large u, and
with f sublinear
for large u, and
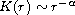 for large r with
for large r with
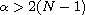 .
We also prove nonexistence if R>0 is sufficiently large.
.
We also prove nonexistence if R>0 is sufficiently large.
