Electron. J. Differential Equations,
Vol. 2017 (2017), No. 135, pp. 1-17.
Data assimilation and null controllability of degenerate/singular
parabolic problems
Khalid Atifi, El-Hassan Essoufi
Abstract:
In this article, we use the variational method in data assimilation
to study numerically the null controllability of degenerate/singular
parabolic problem
![$$\displaylines{
\partial _{t}\psi - \partial_{x}(x^\alpha\partial _{x}\psi(x))
-\frac{\lambda }{x^{\beta }}\psi=f,\quad (x,t)\in ]0,1[\times]0,T[,\cr
\psi(x,0)=\psi_0, \quad \psi\big|_{x=0}=\psi\big|_{x=1}=0.
}$$](gifs/aa.gif)
To do this, we determine the source term f with the aim of obtaining
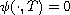 ,
for all
,
for all
![$\psi_0 \in L^2(]0,1[)$](gifs/ac.gif) .
This problem can be formulated in a least-squares framework, which
leads to a non-convex minimization problem that is solved using a
regularization approach. Also we present some numerical experiments.
.
This problem can be formulated in a least-squares framework, which
leads to a non-convex minimization problem that is solved using a
regularization approach. Also we present some numerical experiments.
Submitted February 24, 2017. Published May 17, 2017.
Math Subject Classifications: 15A29, 47A52, 93C20, 35K05, 35K65, 35K65, 93B05.
Key Words: Data assimilation; null controllability; regularization;
heat equation; inverse problem; degenerate equations; optimization.
Show me the PDF file (331 KB),
TEX file for this article.
 |
Khalid Atifi
Laboratoire de Mathématiques
Informatique et Sciences de l'ingénieur (MISI)
Université Hassan 1
Settat 26000, Morocco
email: k.atifi.uhp@gmail.com
|
|---|
 |
El-Hassan Essoufi
Laboratoire de Mathématiques
Informatique et Sciences de l'ingénieur (MISI)
Université Hassan 1
Settat 26000, Morocco
email: e.h.essoufi@gmail.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
\partial _{t}\psi - \partial_{x}(x^\alpha\partial _{x}\psi(x))
-\frac{\lambda }{x^{\beta }}\psi=f,\quad (x,t)\in ]0,1[\times]0,T[,\cr
\psi(x,0)=\psi_0, \quad \psi\big|_{x=0}=\psi\big|_{x=1}=0.
}$$](gifs/aa.gif)
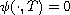 ,
for all
,
for all
![$\psi_0 \in L^2(]0,1[)$](gifs/ac.gif) .
This problem can be formulated in a least-squares framework, which
leads to a non-convex minimization problem that is solved using a
regularization approach. Also we present some numerical experiments.
.
This problem can be formulated in a least-squares framework, which
leads to a non-convex minimization problem that is solved using a
regularization approach. Also we present some numerical experiments.

